Giơi thiệu Thuật toán leo đồi (Hill Climbing Search)
Trước hết, ta nghiên cứu bài toán sau: Trò chơi n2-1 số (n thuộc N, n > 1).
Bài toán:
Có n2-1 số mang các giá trị từ 1 tới n2-1 được sắp xếp vào một lưới các ô vuông kích thước n x n. Mỗi số đó được gọi là một quân cờ và lưới ô đó được gọi là bàn cờ. Có một vị trí của bàn cờ bỏ trống. Mỗi lần di chuyển quân, người chơi được phép chuyển một quân ở vị trí ô tiếp giáp cạnh với ô trống vào ô trống.
Yêu cầu:
Từ một trạng thái ban đầu (sự sắp xếp ban đầu của các quân trên bàn cờ), hãy thực hiện các nước đi hợp lệ để thu được trạng thái kết thúc (trạng thái đích cần đạt được).
Vídụ: với trò chơi 8 số ta minh họa trạng thái ban đầu và trạng thái kết thúc qua các hình vẽ dưới đây:
Hình 1
Để giải bài toán này, chúng ta sẽ nghĩ ngay tới việc xây dựng một cây tìm kiếm mà gốc của cây tương ứng với trạng thái xuất phát của bàn cờ. Các đỉnh khác của cây tương ứng với các trạng thái thu được do việc thực hiện các nước đi hợp lệ (các nước đi được phép thực hiện là: lên trên, xuống dưới, sang trái và sang phải). Với ví dụ trên, ta có cây tìm kiếm sau:
Hình 2
Ý tưởng thuật toán:
Việc suy nghĩ như trên xem ra có tính khả thi (đơn giản, dễ cài đặt), tuy nhiên, dễ nhận thấy rằng nếu số n lớn hơn, ta sẽ phải phát triển một số quá lớn các trạng thái trước khi phát hiện ra trạng thái đích. Những hạn chế về mặt thời gian và dung lượng bộ nhớ không cho phépthực hiện điều đó.
Trong thực tế, có nhiều bài toán mà số các trạng thái của nó là rất lớn (như cờ vua, cờ tướng...), thì việc giải bài toán chỉ có thể thực hiện nếu bằng một cách nào đó ta lược bỏ những trạng thái thừa, không cần thiết nhằm giảm số lượng trạng thái cần phát triển. Để làm được điều đó, phải sử dụng khéo léo các thông tin phản hồi nảy sinh trong quá trình tìm kiếm (các thông tin này còn gọi là thông tin cảm tính: HeuristicInformation). Cách làm này được đưa ra nhằm mục đích lựa chọn được hướng tìm kiếm tốt nhất tại mỗi bước theo nghĩa: hướng đi đó nhanh dẫn tới trạng thái đích nhất và nhằm giảm công sức tìm kiếm.
Thuật toán leo đồi:
Thuật toán tìm kiếm leo đồi đã đáp ứng được yêu cầu trên. Nội dung thuật toán được mô tả như sau:
Bước 1: Nếu trạng thái đầu trùngvới trạng thái đích thì dừng ngay, ngược lại thì chuyển sang bước 2.
Bước 2: Sử dụng các quy tắc biến đổi để tạo ra 1 tập hợp các trạng thái từ trạng thái hiện thời (trong bài toán trên ta có 4 quy tắc biến đổi tương ứngvới 4 phép di chuyển quân).
Bước 3: Với mỗi trạng thái trong tập hợp vừa tạo ra kiểm tra xem đó có phải là trạng thái đích hay không? Nếu phải thì ngừng việc tìm kiếm, nếu không phải thì ta kiểm tra xem trạng thái mới này có tốt hơn (gần trạng thái đích hơn) so với trạng thái đã có hay không? Nếu quả thật như vậy thì ghi nhận trạng thái này, ngược lại thì bỏ qua.
Bước 4: Trong các trạng thái được tạo ra (sau khi thực hiện các thao tác ở bước 3), ta ưu tiên phát triển trạngthái tốt nhất (trạng thái tốt nhất là trạng thái có tiềm năng dẫn tới đích nhanh nhất).
Bước này nhằm mục đích chuyển hướng tìm kiếm lời giải nhanh đến đích nhất.
Bước 5: Lặp lại từ bước 2.
Đến đây bạn có thể nhận thấy thuật toán tìm kiếm leo đồi thực chất là thuật toán tìm kiếm theo chiều sâu, song tại mỗi bước ta sẽ ưu tiên chọn một trạng thái có hứa hẹn nhanh tới đích nhất để phát triển trước. Vấn đề quan trọng là ở chỗ biết khai thác khéo léo thông tin phản hồi để xác định hướng đi tiếp và đẩy nhanh quá trình tìm kiếm.Thông thường ta gắn mỗi trạng thái của bài toán với một số đo (1 hàm đánh giá) nào đó nhằm đánh giá mức độ gần đích của nó.
Như vậy: Nếu trạng thái hiện thời là u, theo bước 4 của thuật toán trên thì trạng thái v sẽ được phát triển tiếp theo nếu vẻ kề(u) và hàm đánh giá của v đạt giá trị max (hoặc min).
Phần tiếp theo sẽ trình bày cụ thể thuật toán để giải bài toán trên. Trong bài toán này, ta sẽ sử dụng hàm đánh giá ký hiệu là h với ý nghĩa: h(u) cho biết số cácchữ số trong trạng thái u không trùng với vị trí của nó trong trạng thái đích.Trạng thái có tiềm năng dẫn tới đích nhanh nhất (được ưu tiên phát triển trước)là trạng thái có hàm đánh giá h đạt giá trị min.
Thuật toán cho trò chơi n2-1 số được mô tả như sau :
Hình 3
Algorithm:
Input: Trạng thái ban đầu u0và trạng thái đích ut
BEGIN
1. P:={u0} ; { P để lưu các trạng thái chờ phát triển được tổ chức dưới dạng Stack }
Q:=Φ ; { để lưu các trạng thái đãphát triển được tổ chức dưới dạng hàng đợi Queue }
P:= Φ ; { P để lưu tạm thời các trạngthái kề với trạng thái đang xét }
found:=false;
2. While (P # y) and (not found) do
2.1. Loại bỏ trạng thái u ở đỉnh stack P và đặt nó vào hàng đợi Q:
Pop(P, u);
Add(u, Q);
2.2. if u=ut then found:= true
else
For v kề (u) do
if (v thuộc P U Q) and (h(v) <= max { h(w)| w thuộc P U Q } then
Begin
father (v):=u;
Add (v, P);
End;
if P <> f then
Begin
- Sắp xếp các trạng thái trong P theotrật tự tăng của hàm h;
- Chuyển các trạng thái trong P vàođỉnh của stack P sao cho trạng thái có giá trị hàm h nhỏ nhất ở đỉnh của P;
End;
END.
Output:
- Nếu found = false thì bài toán không có lời giải.
- Nếu found = true thì lời giải là đường đi từ u0 tới ut được xác định bằng cách sử dụng hàm father.
Chú ý: Sau khi chuyển các trạng thái từ P vào P thì P= f
Hình 4
h(v1) ≤ h(v2) ≤ .... ≤ h(vk)
Với ví dụ trên, cây tìm kiếm được hình thành bởi tìm kiếm leo đồi có các trạng thái được phát triển như hình vẽ dưới (nét đậm thể hiện hướng tìm kiếm), các số ghi cạnh mỗi đỉnh là giá trị của hàm h tại đỉnh đó.
Thuật toán này có tên gọi là thuật toán tìm kiếm leo đồi, vì tư tưởng của nó tương tự như trường hợp: Một người ở vị trí chân đồi u0 và muốn leo lên đỉnh đồi tại vị trí ut. Anh ta chọn một đỉnh cao nhất trong số các đỉnh mà anh ta có thể đến được (từ vị trí đang đứng) để leo lên, tại vị trí này anh ta lại chọn một đỉnh cao nhất như bước trước để leo lên. Quá trình cứ lặp lại như vậy cho đến khi tới được đích ut.
Nhận xét: Thuật toán này đơn giản, dễ cài đặt và tỏ ra có nhiều hiệu quả. Bạn đọc có thể tự lập trình để giải bài toán trên, kết quả khá tuyệt vời! Tuy nhiên, thuật toán này không phù hợp với các bài toán có giá trị hàm đánh giá đột nhiên thay đổi khi đến ngưỡng nào đó. Một số hiện tượng sẽ nảy sinh trong quá trình tìm kiếm được ghi nhận như sau:
*Có cực đại địa phương, là nơi đạt được lời giải tốt hơn các lời giải lân cận, nhưng chưa phải là lời giải tốt trên tổng thể. Như vậy phải có biện pháp ghi nhớ lại nhiều đường đi đề phòng khi cần đi lại đường cũ.
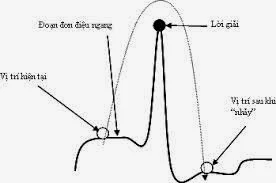
*Có vùng lời giải như cao nguyên bằng phẳng, không thể xác định được ngay hướng nào tốt hơn nếu chỉ so sánh vùng lân cận (các trạng thái của bài toán có hàm đánh giá xấp xỉ bằng nhau). Khi đó cần có bước nhảy xa để thoát khỏi vùng bằng phẳng.
Có đỉnh hình chóp, đó là trạng thái được lựa chọn tốt hơn vùng lân cận nhưng không vượt qua được theo bất kỳ hướng nào. Để xử lý hiện tượng này, nên chuyển theo đồng thời vài hướng.
Cực đại địa phương Cao nguyên Chóp
Minh họa cực trị địa phương khi giải bài toán bằng thuật toán leo đồi.
Như vậy: Thuật toán này chỉ làphương pháp giải quyết cục bộ, để tăng tính tối ưu, có thể sử dụng phối hợp nóvới các thuật toán tìm kiếm khác.
Hình 5
Có thể bạn quan tâm:
Tham khảo 123doc